Donald Eastman III, the president of Eckert College, wrote about the limits of online learning: “…what works for most students…is a small classroom…where a respected authority…is a spellbinding revealer of mysteries – not simply because he or she knows things we don’t, but because a gifted teacher reads the audience the way an actor reads the room…”
The University of Toronto announced that it had joined Coursera. In response, Clifford Orwin, a professor of political science at the U of T, wrote in The Globe and Mail that “the classroom experience is at the heart of education…The electricity that crackles through a successful classroom can’t be transmitted electronically.”
Pamela Hieronymi in her essay in the Chronicle of Higher Education declared that the capacities of online technology “should not be confused with the training provided by one mind interacting with another.”
In short, the chorus of critics is that online and virtual is a shoddy imitation of the real thing. Such declarations miss the point. They are assertions that the ideal traditional classroom is the real criterion against which online should be compared, rather than simply serving as a reference point for comparison with other alternatives.
The issue of whether the new technologies are consistent with a hypothetical ideal appropriate for the specific circumstance of lecturing to a captive audience at a fixed time and place is a meaningless theoretical exercise. The essential exercise is to compare this particular circumstance with other circumstances using an objective external standard.
The objective standard at one extreme is a situation in which hardly anyone learns anything. At the other extreme is one in which almost everyone learns everything. These two limiting distributions can be plotted on a graph in which the X-Axis is the proportion of the material learned and Y-Axis is the proportion of the class.
In practice, of course, both limits can only be approached. Every class results in an actual distribution defined by the standard deviation around the average amount learned. The distribution for any class can be plotted on the same graph as the two limiting cases. This simple graphic provides an objective external standard for comparisons between different circumstances and different teaching methods. The only question is, on the average, how close does any particular effort approach a limit, and what is the spread between the students who are most and least successful?
The now classic example of this kind of research has been carried out over the past several decades on the teaching of large enrollment introductory physics classes. Typically, students in these classes could calculate answers to problems using formulas, but they were unable to apply the concepts to answer basic questions.
Harvard Professor Eric Mazur found that after a semester of lecturing, on the average, students understood at best about 30% of the material. However, 60% understood the material when it was presented online, and the classroom was “flipped” to practice applying the concepts in small discussion groups. (NPR)
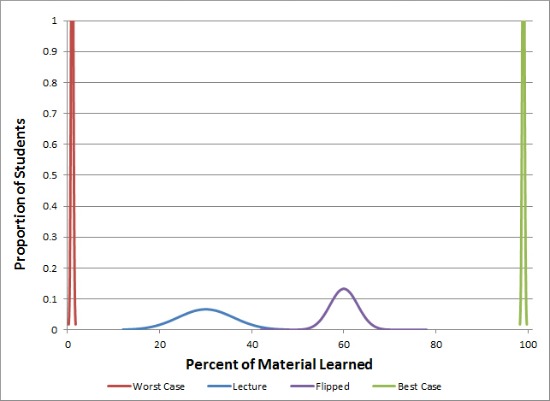
Professor Carl Wieman of the Science Education Initiative at the University of British Columbia has carried out controlled experimental studies on this method. In a study published in Science he found that the online presentation of the material followed by peer group discussions in the classroom more than doubles the average amount of material mastered. In addition, 90% of the students reported enjoying the interactive teaching techniques more than traditional lectures; while only 1% disagreed and the other 8% were indifferent. In addition, levels of student engagement and attendance were significantly higher with the flipped classroom.
This is the type of information that needs to be informing policy discussions over the relative effectiveness of different circumstances and methods of teaching, not declarative statements comparing the new digital communication techniques with a hypothetical theoretical classroom.
What is of theoretical importance is identifying the practical teaching practices that account for the means and standard deviations of the distributions of actual students, under different specific circumstances. The result for different groups provides comparative empirical reference points; none of which are an ultimate criterion.
We might speculate that when experienced professors interacted with students personally known to them in small classes, that the average amount learned was greater compared to today’s large lecture classes, often taught by overworked adjunct professors who do not have on-campus offices. Also, we might reasonably speculate that a technologically challenged professor would do much worse trying to teach online than face-to-face, no matter how large the face-to-face class.
It is these types of speculations that are of great theoretical importance. They can be empirically identified and dealt with strategically by doing the best job possible with the resources we have. These differences will not be addressed, however, by refusing to accept responsibility for any change in light of the many new circumstances and teaching methods now available.
We need to recognize that the art and science of teaching and learning in the 21st Century is now different. Our challenge is how to systematically go about using the new technologies to enhance teaching and learning without making declarative statements based on our beliefs, as if they were something more than just that. We have the capacity to reflectively apply the science and critical thinking we teach our students to what we ourselves are actually doing. Our own classrooms are the ideal place to demonstrate the power of scientific inquiry and critical thinking that we claim to be our non-replaceable purpose as teachers.
Dr. Edward Renner teaches in the Honors College at the University of South Florida.
Reference:
Deslauriers, L., Schelew, E., & Wieman, C. (2011). Improved Learning in a Large-Enrollment Physics Class. Science, 332 (6031), 862-864. http://www.sciencemag.org/content/332/6031/862





